전달함수 $G(s)$로 표현되는 시스템의 bode plot 해석을 진행할때 중요한 assumption이 있습니다.
바로 해당 전달함수가 안정 (open left half plane 에 모든 극점 존재) 해야한다는 점인데요.
두가지 실제 상황을 보면서 얘기해보겠습니다.
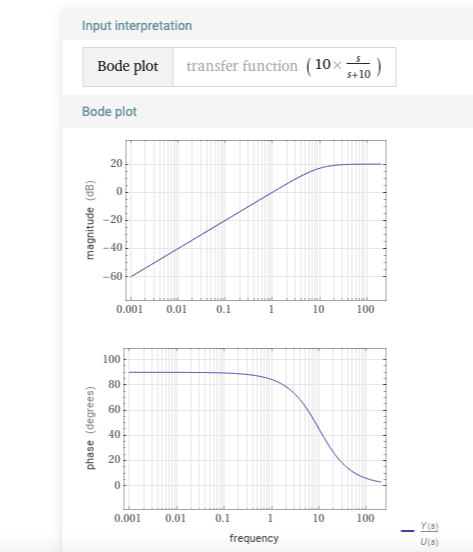
먼저 안정한 시스템 $G_{1}(s) = \frac{10s}{s+10}$ (극점 s = -10)의 bode plot입니다. 여기에다가 각주파수 5rad/s를 가지는 정현파 입력 $x(t) = cos(5t)$을 가하겠습니다. $\mathcal{L}\{x(t)\} = \frac{s}{s^2+25}$ 입니다.
그럼 시스템 출력은 $\mathcal{L^{-1}}\{\frac{10s}{s+10} * \frac{s}{s^2+25}\}$ 가 되겠습니다.
그리고 시스템의 정현파 입력 해석법에 의하여 또한 $y_{steady}(t) = |G_{1}(5j)|cos(5t + \angle {G_{1}(5j)})$ 인데요.
가장 간단하게 보드플롯에서 $|G_{1}(5j)|$와 $\angle{G_{1}(5j)}$ 값을 바로 알아낼 수 있습니다.
frequency = 5에서 13dB, $63^{\circ}$ 정도 나오네요 제가 지금 매트랩이 없어서 울프람에서 어림짐작으로 찾고 있네용..ㅎㅎ
그러면 $y_{steady}(t) = 10^{\frac{13}{20}}cos(5t + 63^{\circ})$ 라고 할 수 있겠군요. 그럼 한번 확인해봅시다.
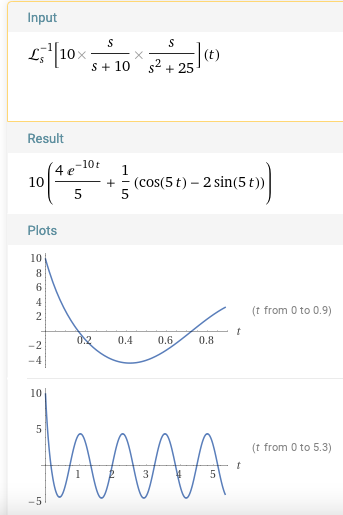
inverse laplace 결과입니다. steady state 상태를 봐야겠죠? 아쉽게도 초기 구간의 다이나믹은 bode plot만으로는 알 수가 없답니다.
t = 2s 에서 steady state로 들어간 것으로 보겠습니다.

어림짐작으로 찾은 output과 inverse laplace의 그래프를 그려보았습니다. 초기구간을 제외하고 steady state에서 그래프가 일치함을 확인할 수 있겠네요. 그래프는 제가 애용하는 desmos로 그려봤는데요 휴대폰 어플로도 있는데 가끔씩 급하게 그래프 그릴 때 굉장히 유용하답니다.
이로써 안정한 시스템의 bode plot의 정현파 입력 분석을 직관적으로 이해할 수 있었습니다. 그런데 불안정 시스템은요???
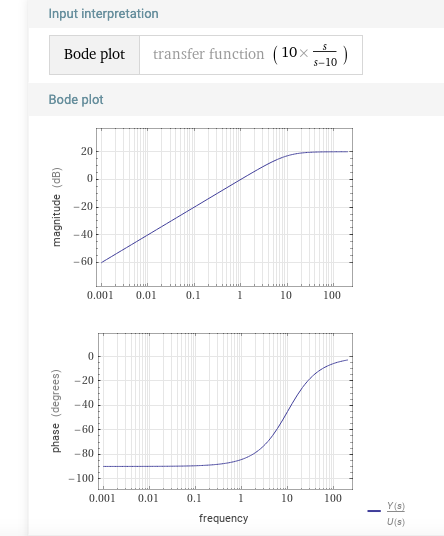
극점이 s = 10에 있는 불안정 시스템 $G_{2}(s) = \frac{10s}{s-10}$의 bode plot 입니다. 그런데 사실요. 위의 $G_{1}(s) = \frac{10s}{s+10}$일 때랑은 위상만 뒤바뀌고 magnitude는 차이가 없습니다. 그런데 우리는 이 시스템이 발산한다는 걸 알고 있습니다. 하지만 발산은 뭔가 magnitude랑 연관이 될 것 같은데 보드플롯의 magnitude는 13dB밖에 안돼서 출력이 무한으로 가지는 못할 것 같은데요!

뭔가 이상하죠. 대답은 불안정 시스템의 bode plot은 좀 다르게 봐야 한다는 것입니다.

이게 제가 구글링으로 찾아온 대답인데요. 간략하게 설명하자면.. 불안정 시스템도 특정 조건(웬만해서 절대 만족될 수 없는??) 하에서 똑같은 분석이 가능하다고 합니다.
앞서 언급했듯이 bode plot은 steady state의 솔루션만을 제공하는데요. 사실 전체 솔루션은 여기에 transient state (과도기 응답, 앞서 실제 Inverse laplace transform 결과에서 $\frac{4e^{-10t}}{5}$ 부분) 까지 포함하고 있습니다. 여기서는 지수항이 음수라서 steady state로 갈 수 있었습니다. 해당 지수항은 0으로 수렴하게 되니까요. 그런데 불안정 시스템이라면 이 지수항이 발산하게 되고 정현파 출력은 상대적으로 보이지 않게 되는 겁니다.
그래서 초기 조건에서 이 지수항의 계수가 0이 되도록 하면 안정한 시스템의 bode plot 분석방법으로 steady state를 찾아낼 수 있습니다. 앞서 했던 과정이랑 똑같아요. 그런데 웬만해서는 이 지수항들의 계수가 전부 0이 되는게 거의 불가능하다고 본답니다.
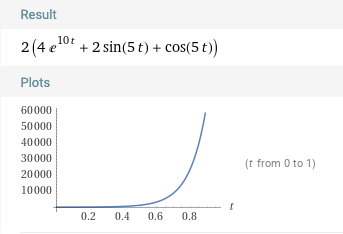
그러니까 위 출력 그래프를 확대해보면.. 사실 정현파가 삐죽삐죽 노이즈처럼 껴있다는 말이죠. 실제 식에서도 삼각함수 항이 멀쩡히 살아있잖아요? 그리고 저 삼각함수 항들은 $y_{steady}(t) = |G_{2}(5j)|cos(5t + \angle {G_{2}(5j)})$를 만족합니다.
그래서 오늘 포스팅의 결론은!! bode plot 분석은 시스템의 안정도와 상관없이 유효하다는 말입니다.
다만 불안정 시스템의 실질적인 출력은 bode plot만으로 판별할 수가 없다는 거네요. bode plot이 솔루션의 정보를 모두 포함하지 않는다는 한계에서 기인한 문제네요. bode plot이 볼 수 없는 사각지대가 엄청~~나게 dominant해질 수 있으니 주의하라는 말씀입니다.
그래서 bode plot만 대충 눈으로 보고 출력을 예측하는 테크닉은 안정한 시스템에서만 유효하다는 것을 알 수 있습니다.
정보가 도움이 되셨으면 좋겠습니다!!!
reference