신시 필수 문제 하나 - 계단 함수를 적분으로 표현하는 법

신시 문제 하나 풀어보고 가겠습니다. 약간 수능식? 사고력을 요하는 문제인데요.

 

왜냐하면 단순 계산문제가 아니라 개념 응용을 요구하는 문제라서요.

 

나름 자주 나와서 유명한 유형같기는 한데, 혹시 아직 접해보시지 않은 분들은 꼭 풀어보시기 바랍니다.

 

이런 유형에 익숙해져야.. 시스템 입출력 관계를 수식 하나로만 던져줘도 모든 입력에 대한 출력을 '정석적인 방법'으로 찾을 수 있습니다.

 

 

 

그럼 문제입니다.

 

 

1. what is the impulse response h(t) for this system?

 

 

- solution -

 

impulse response는 입력을 impulse 함수로 넣었을 때의 출력을 찾으라는 말이죠.

 

 

즉 입력 $x(t)$가 $\delta (t)$일 때의 $y(t)$를 찾으라는 뜻입니다.. 그러면 저희가 찾는 $y(t)$는

 

 

$y(t)={\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}\delta (\tau +2)d\tau$ 입니다.

 

 

$(\tau +2)$ term이 거슬리니까 $\tau +2=k$ 로 치환합시다. 그러면 해당 적분은

 

 

$y(t)={\int }_{-\mathrm{\infty }}^{t+2}{e}^{-(t-k+2)}\delta (k)dk$ 형태가 됩니다.

 

 

적분상수는 $\tau$니까요, $e^{-(t+2)}$ term은 적분 밖으로 빼줍니다. 

 

 

그러면 $y(t)=e^{-(t+2)}{\int }_{-\mathrm{\infty }}^{t+2}{e}^k\delta (k)dk$ 입니다.

 

 

적분항인 ${\int }_{-\mathrm{\infty }}^{t+2}{e}^k\delta (k)dk$ 는 곧 ${\int }_{-\mathrm{\infty }}^{t+2}\delta (k)dk$입니다.

(impulse 함수의 sampling 특성)

 

 

그래서 $y(t)=e^{-(t+2)}{\int }_{-\mathrm{\infty }}^{t+2}\delta (k)dk$네요.

 

 

여기서부터가 중요한데요.

 

 

적분항 ${\int }_{-\mathrm{\infty }}^{t+2}\delta (k)dk$ 의 값은 t값에 따라 달라집니다. 왜냐하면 적분 구간이 임펄스를 포함하는지의 여부가 적분값을 결정하거든요. 적분 구간이 임펄스를 포함하면 1, 그렇지 않다면 0일 것입니다.

 

즉 

               $${\int }_{-\mathrm{\infty }}^{t+2}\delta (k)dk=\{\begin{array}{ll}1& (t+2)\ge 0\\ 0& (t+2)<0\end{array}$$

 

인데요 뭔가 익숙하시지 않나요??~~ 딱 보면 step function이라는 것을 알 수 있습니다.

 

위 식은 다름아닌 $\mu (t+2)$입니다.

 

임펄스 함수와 적분 구간의 조합으로 저렇게 평행이동된 step function을 만들어낼 수 있습니다. 이게 가장 중요한 점이에요.

 

그럼 $y(t)=e^{-(t+2)}{\int }_{-\mathrm{\infty }}^{t+2}\delta (k)dk$ 에서 적분항 결과가 나왔으니, 해당 결과에 $e^{-(t+2)}$만 곱해주면

 

$$y(t)=\{\begin{array}{ll}{e}^{-(t+2)}& (t+2)\ge 0\\ 0& (t+2)<0\end{array}$$

 

$y(t)=e^{-(t+2)}\mu (t+2)=h(t)$ 가 되겠습니다.

 

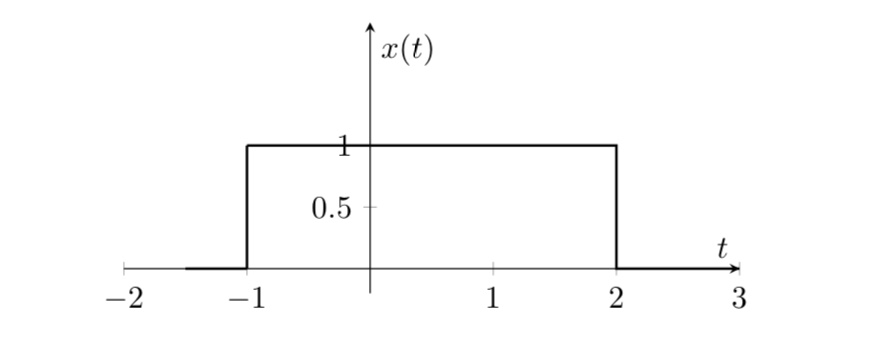
2. Determine the response of the system when the input $x(t)$ is as shown in the following figure.

- solution - 

 

(첫번째 방법, 정석적 풀이)

 

 

$x(t)=\mu (t+1)-\mu (t-2)$

 

 

주어진 $x(t)$를 시스템 방정식에 그대로 대입합니다.

 

 

$y(t)={\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}(\mu (\tau +3)-\mu (\tau ))d\tau$

 

 

$y(t)={\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}\mu (\tau +3)d\tau -{\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}\mu (\tau )d\tau$

 

 

step functon은 유효 적분구간을 축소시킵니다.

 

 

$y(t)={\int }_{-3}^t{e}^{-(t-\tau )}d\tau -{\int }_0^t{e}^{-(t-\tau )}d\tau$

 

 

해당 적분 결과는 

 

 

$y(t)=(1-e^{-(t+3)})\mu (t+3)-(1-e^{-t})\mu (t)$ 입니다.

 

 

첫번째 방법은 1번 문제의 솔루션과 같은 흐름입니다. 필요한 입력을 주어진 시스템 방정식에 넣어서 계산하는거죠.

 

 

(두번째 방법)

 

 

사실 step function에 대한 응답은 impulse 응답의 적분입니다. $h(t)$는 1번 문제에서 찾아놨죠?

 

 

즉 $y_{step}(t)={\int }_{-\mathrm{\infty }}^{t}h(t)dt=(1-e^{-(t+2)})\mu (t+2)$ 

 

 

$x(t)=\mu (t+1)-\mu (t-2)$

 

 

$y(t)=y_{step}(t+1)-y_{step}(t-2)$

 

 

$y(t)=(1-e^{-(t+3)})\mu (t+3)-(1-e^{-t})\mu (t)$

 

 

 

문제를 풀어보셨으면 '정석적인 방법'이 무엇을 의미하는지 이해하실 수 있으실 겁니다. 입력과 시스템 방정식이 아무리 복잡하게 생겨도 대입해서 계산하면 출력이 나온다!! 이게 바로 시스템입니다. 다만 1번 문제의 경우 적분 결과가 조금 생소하게 느껴질 수 있는데, step function을 규정하는 저 방법은 숙지해놓으시면 좋을 것 같습니다.

 

 

 

 

+ 추가문제

 

 

거의 똑같은 문제인데, 한 단계만 추가하면 됩니다. 해당 단계에 대한 힌트만 숨겨놓고 가겠습니다 ㅎㅎ

 

 

- hint - 

 

 

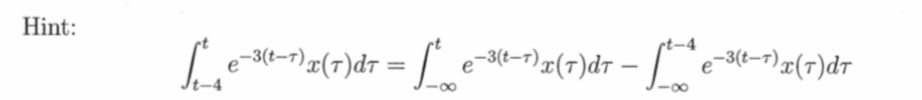
다음 단계는 뭔지 다 아시겠죠? ㅎㅎㅎ

 

 

 

 

 

 

 

 

 

 

문제 출처 EEE20501 Signall & System 2022 midterm (UNIST),

BLM2401 Signals and Systems midterm (Yıldız Technical University)