RMS의 실질적인 의미를 알아보자! RMS를 왜 계산하고 사용하는가?
교류 AC전압을 처음 배울 때 RMS라는 개념이 등장합니다.
RMS는 Root Mean Square의 약자입니다.
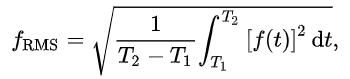
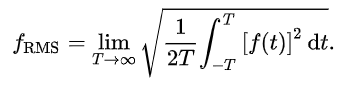
구하는 식은 꽤나 직관적입니다. 말 그대로 Root (of) Mean (of) Square라고 할 수 있겠는데요.
제곱의 / 평균의 / 루트입니다. (of)의 존재를 의식하면 식 외우기도 간편합니다.
그런데 RMS의 공식 자체는 쉽지만 이것이 왜 중요한지는 잘 알려주지 않는 것 같습니다.
그러면 왜 교류를 배우는데 RMS를 알아야 했는가?
RMS는 "평균적으로 공급되는 양"을 알려줍니다.
그런데 중요한 것은!! 여기서 "평균적으로 공급되는 양"은 전력의 양을 의미한다는 것입니다.

일례로, 계산해보면 상수함수는 임의의 구간에서 평균과 RMS값이 동일합니다. 해당 상수값이 $K$라면 그대로 $K$가 평균이자 또한 RMS입니다.
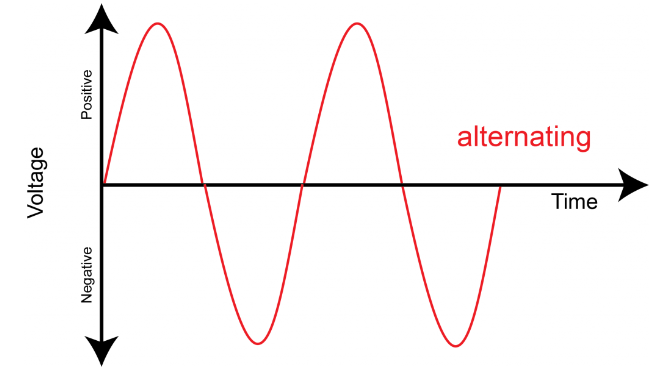
Sine함수는 평균이 0이지만 Sine함수를 제곱하면 적분값이 양수가 되어 RMS를 계산할 수 있습니다.
앞서 RMS는 "평균적으로 공급되는 전력"을 알려준다고 했습니다.
단순 저항 부하에 전압이든 전류든 입력을 넣어준다고 합시다.
이 때 임의의 파형을 갖는 입력이 만들어내는 전력은,
해당 파형의 "RMS값과 동일한 직류 입력"이 만들어내는 전력과 같습니다.
특정 구간에서 평균 전력의 계산식을 한번 봅시다.
$P = \frac{1}{T_{2}-T_{1}}\int_{T_{1}}^{T_{2}}v(t)i(t) dt$입니다.
저항 부하에서는 $v(t)$와 $i(t)$의 파형이 동일하고 동일한 파형끼리 곱하면 제곱 항이 생기게 됩니다.
전압 입력 $v(t)$와 부하 저항 $R$이라 두면 $i(t) = \frac{v(t)}{R}$입니다.
RMS 공식에 의해 $v_{rms}^{2} = \frac{1}{T_{2}-T_{1}}\int_{T_{1}}^{T_{2}}v(t)^{2}{dt}$입니다.
그렇다면 $P = \frac{v_{rms}^{2}}{R}$임을 알 수 있습니다. $i_{rms}$에 대해서도 $P = i_{rms}^{2}R$을 동일한 방식으로 도출할 수 있습니다.
즉 우리에게 익숙한 식 $P = I^{2}R$ 및 $P = \frac{V^{2}}{R}$ 와 $P = IV$은 (대문자는 직류 입력을 의미)
임의의 파형 입력에 대해서 $P = i_{rms}^{2}R$ 및 $P = \frac{v_{rms}^{2}}{R}$ 와 $P = i_{rms}v_{rms}$으로 일반화됩니다.
공식에 RMS값을 넣어야 직류 $\rightarrow$ 임의의 파형으로 일반화가 된다는 것이죠.
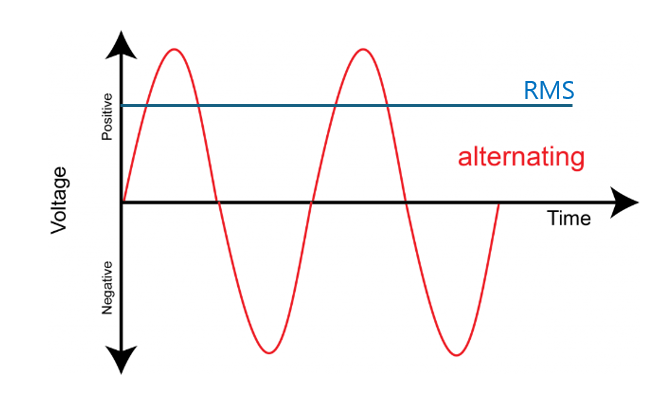
그림으로 보이자면 위의 두 파형이 저항 부하에서 동일한 전력을 만들어낸다는 뜻입니다.
다시 한 번 정리하자면,
임의의 파형을 갖는 입력이 만들어내는 전력은, "해당 파형의 RMS값과 동일한 직류 입력"이 만들어내는 전력과 같습니다.
RMS는 다분히 전력의 관점에서 편하게 생각하기 위해 계산하는 값입니다.
하나의 직류 값으로 대치해서 전력 양을 생각할 수 있다는 것이죠.
이제 RMS만 계산하면 임의 파형의 입력이 갖는 전력을 계산할 수 있는 것입니다.

이런 괴이한 모양의 입력 전류에 대해서도 전력을 쉽게 계산할 수 있습니다.
추가로 제가 위에서 "저항 부하 조건"을 언급했는데
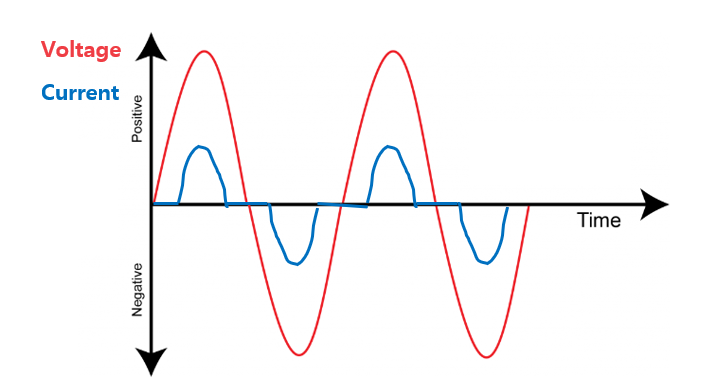
비저항 부하 조건에서는 이처럼 전압과 전류의 파형이 맞지 않거나 위상이 달라지는(LC 부하) 상황이 생기는데요.
여기서 RMS값으로 계산되는 전력은 유효전력과 무효전력의 합, 즉 피상젼력이 됩니다.
즉 $P+Q = i_{rms}v_{rms}$입니다.
RMS값으로 전력을 계산하는 원리는 동일하나
비저항 부하에서는 계산된 전력의 유효 및 무효분을 추가로 분석해야합니다.
이에 대해서는 다음 포스팅에서 다루도록 하겠습니다.
이번 포스팅도읽어주셔서 감사합니다!!
'전력전자' 카테고리의 다른 글
| 벅 컨버터 전압 제어 모드 (Voltage control mode) (3) | 2024.06.28 |
|---|---|
| 변압기의 자화 인덕턴스(Magnetizing Inductance)는 무엇인가 (0) | 2024.06.26 |
| 풀업 / 풀다운 저항(Pull up/down resistor)의 트랜지스터 구현, 과전압 보호 회로 (1) | 2024.04.07 |
| 컨버터의 소프트 스위칭 ZVS(Zero voltage switching) (1) | 2024.02.09 |
| Forward 컨버터 뿌수기 (2) - 입출력 전압 전류 파형과 공식 (0) | 2024.01.01 |