오늘은 DC컨버터의 전압 제어 모드에 대해 알아보겠습니다.
안녕하세요 Brandy입니다.
DC컨버터의 기본 원리와 토폴로지들을 공부하고 나면 다음 단계(아주 거대한..)가 남아있습니다.
바로 컨버터의 피드백 루프인데요.
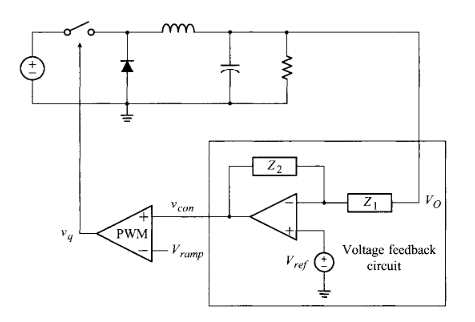
이렇게 벅 컨버터에 op amp회로가 붙어있는 것을 보실 수 있습니다!! Voltage feedback circuit이라고 적혀 있습니다.
즉 위와 같이 출력 전압을 제어하기 위해서 기본 컨버터 토폴로지에 feedback 회로를 추가하게 됩니다.
벅 컨버터는 PWM의 듀티비에 따라 출력 전압이 변동합니다.
입출력 전압 관계는 $V_{out} = DV_{in}$으로 표현되는데요.
컨버터가 동작하는 과정에서 입력 전압 변동이나 부하 변동 등의 외란이 발생할 수 있습니다.
이런 외란에 맞서 출력 전압이 출력 지령값 $V_{ref}$을 유지하도록 제어할 수 있어야 합니다.
바로 이를 가능하게 하는 것이 바로 피드백 회로입니다.
오늘은 가장 간단한 컨버터 제어법인 전압 제어 모드를 설명해보도록 하겠습니다.
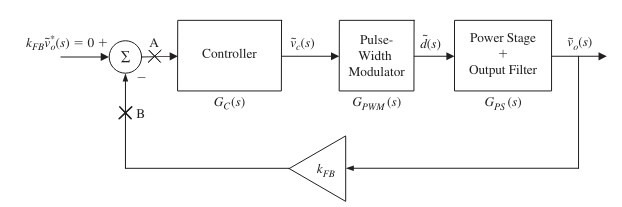
피드백 회로까지 추가한 컨버터를 위와 같이 블록 다이어그램으로 표현했습니다.
간단하게 플랜트 $G_{PWM}(s)G_{PS}(s)$와 컨트롤러 $G_{c}(s)$, 그리고 Feedback gain인 $k_{FB}$로 구성됩니다.
$k_{FB}$은 출력 전압의 측정 과정에서 상수가 곱해질 수 있음을 의미하는데 여기서는 1입니다. (회로에서 $V_{o}$가 Op amp에 그대로 들어감을 확인하세요)
이제 각 블럭의 전달함수와 작동 원리를 알아봅시다.
먼저 가장 쉬운 $G_{PWM}$블록부터 시작하겠습니다.
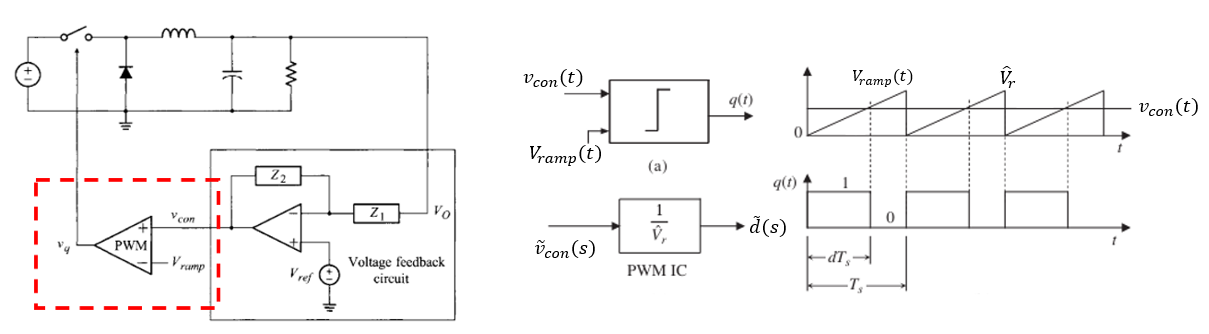
앞서 Buck 컨버터가 PWM 듀티 비로 출력 전압을 결정한다고 했습니다. 실제 PWM은 어떻게 만들어지는 것일까요?
위 그림처럼 PWM에는 비교기와 주기적 램프 신호인 $V_{ramp}$가 필요합니다.
비교기는 $V_{ramp}$와 컨트롤 지령값인 $v_{con}$를 비교하여 $v_{con} > V_{ramp}$일 때 On 신호를 내보내게 됩니다.
따라서 오른쪽 그림과 같이 주기적으로 펄스를 내보내는 것이죠.
$G_{PWM}(s)$의 전달함수는 단순히 $\frac{\tilde{v}_{c}(s)}{\tilde{d}(s)} = \frac{1}{\widehat{V}_{r}}$입니다. $\widehat{V}_{r}$는 램프 신호의 피크값입니다.
일반적으로 $\widehat{V}_{r} = G_{PWM}(s) = 1$입니다.
만약 입력 전압 $V_{in} = 10V$에 출력 지령값 $V_{ref} = 5V$라면 제어가 적절히 이루어질 때 자동으로 $v_{con} = 0.5V$가 맞춰질 것입니다.
PWM에 대해서 더 알고 싶으시다면 아래 포스팅을 참고해주세요. PWM에 사용되는 ramp신호의 종류와 회로 구현법을 다룹니다.
2024.07.04 - [전력전자] - PWM 제어, 펄스폭 변조의 개념과 회로 구현
PWM 제어, 펄스폭 변조의 개념과 회로 구현
PWM(Pulse-Width Modulation)제어의 개념과 실제 회로 구현법을 알아봅시다. 안녕하세요 Brandy입니다. 오늘은 PWM제어가 무엇인지, PWM제어는 어떤 소자들을 통해 실제로 구현할 수 있는지 공부해보겠습
brandy2000.tistory.com
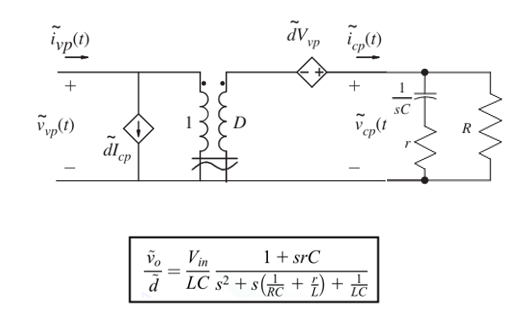
다음으로 $G_{PS}(s) = \frac{\tilde{v}_{o}(s)}{\tilde{d}(s)}$는 벅 컨버터의 파워 스테이지입니다.
파워 스테이지는 "듀티비의 소신호 변동에 따른 출력 전압의 변동"을 의미합니다.
대신호(직류) 모델에서 듀티비와 전압의 관계식 $\frac{V_{o}}{D} = V_{in}$입니다만, 소신호 전달함수를 찾기 위해서는 벅 컨버터의 소신호 모델이 필요합니다.
소신호 모델과 여러 전달함수의 유도는 다른 포스팅에서 다루도록 하겠습니다. 여기서는 일단 결과만 보이도록 합니다.
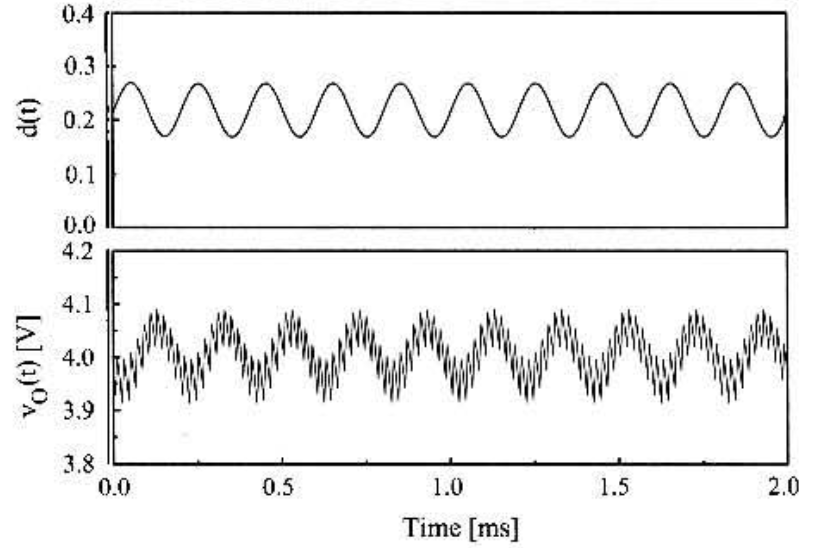
듀티비의 소신호 변동에 따른 출력 전압의 변동이라 함은, 위의 파형으로 직관적인 이해를 할 수 있습니다.
전달함수를 가지고 정현파 $d(t)$ 입력에 따른 $v_{o}(t)$를 찾을 수 있습니다. $v_{o}(t)$의 삐죽삐죽한 부분은 스위칭 리플입니다. 벅 컨버터에서 ON/OFF 상태에 따라 전류가 상승과 하강을 반복하는 부분이죠.
리플을 제외한 전체적인 carrier 모양은 주파수 응답으로 해석할 수 있습니다.
그리고 벅 컨버터의 플랜트 전달함수 $G_{PWM}(s)G_{PS}(s)$는 다음과 같이 생겼습니다. 앞서 주어진 전달함수에 적절한 파라미터를 넣어서 보드 플롯을 그려 보세요.
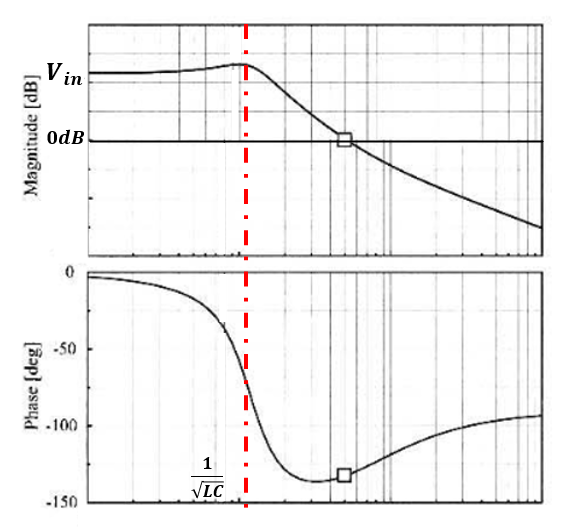
$G_{PS}(s)$의 형태를 보면, 페이즈가 double pole 다음 single zero를 거치는 것을 확인할 수 있습니다.
그리고 이제 해당 플랜트를 컨트롤러 $G_{c}(s)$를 가지고 보상할 수 있습니다. 기본적으로 2차 시스템의 컨트롤러 디자인이기 때문에 자동제어를 공부하셨다면 어렵지 않으실 겁니다.
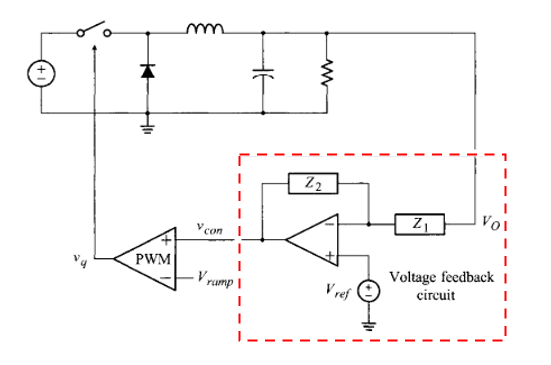
다시 컨트롤러로 돌아옵시다. OP amp로 컨트롤러를 디자인하려면 어떻게 해야 할까요?
먼저 위 그림에서 $\frac{V_{con}-V_{ref}}{Z_{2}(s)} = -\frac{V_{o}-V_{ref}}{Z_{1}(s)}$입니다. (Ideal OP amp)
즉 $\frac{Z_{2}(s)}{Z_{1}(s)}(V_{o} - V_{ref}) = V_{ref} - v_{con}$인데
계단 응답 Steady state 에러를 0으로 만들기 위해 컨트롤러 전달함수는 $\frac{1}{s}$를 포함해야 합니다.
소신호 모델에서 대신호(DC값)는 0으로 처리합니다. 전류 지령값 $V_{ref}$은 대신호로 보겠습니다.
$V_{ref} = 0$이면 $G_{c}(s) = \frac{\tilde{v}_{con}(s)}{\tilde{V}_{o}(s)} = -\frac{Z_{2}(s)}{Z_{1}(s)}$이기 때문에
$Z_{2}(s)$가 적분기($\frac{1}{s}$)를 포함해야 하네요.
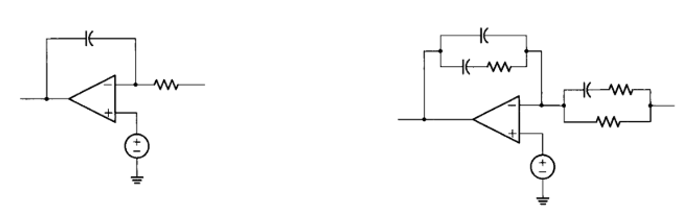
적분기를 포함한 가장 간단한 컨트롤러는 Miller integrator입니다. 또는 PI 컨트롤러를 써도 되겠습니다.
그런데 이 두 컨트롤러는 계단 응답의 Steady state 에러를 0으로 만들기는 하겠지만, 보상 과정에서 Transient response를 개선하기는 어려울 수 있습니다.

Transient response의 개선을 위해 $G_{PS}(s)$의 Phase margin과 Crossover Frequency를 최대화하도록 컨트롤러를 디자인해야합니다.
이를 위해 3p2z나 Type I, II, III등의 컨트롤러를 사용할 수 있습니다.
참고로, 전압 제어 모드는 주로 벅 컨버터의 제어에 활용됩니다.
앞서 봐왔던 벅 컨버터의 파워 스테이지와 달리, 부스트나 벅-부스트 컨버터의 파워 스테이지는 전압 제어 모드로 보상하는데 무리가 있습니다.
해당 컨버터들에는 전류 제어 모드라는 다른 제어기법을 적용할 수 있습니다. 기회가 되면 다음에 다루도록 하겠습니다.
이번 포스팅도 읽어주셔서 감사합니다!!
'전력전자' 카테고리의 다른 글
| 정류기 전류 고조파 발생원리 (0) | 2024.08.11 |
|---|---|
| PWM 제어, 펄스폭 변조의 개념과 회로 구현 (0) | 2024.07.04 |
| 변압기의 자화 인덕턴스(Magnetizing Inductance)는 무엇인가 (0) | 2024.06.26 |
| RMS(실효값)의 실질적 의미 (0) | 2024.06.21 |
| 풀업 / 풀다운 저항(Pull up/down resistor)의 트랜지스터 구현, 과전압 보호 회로 (1) | 2024.04.07 |